Iris මල් දත්ත කට්ටලය
අයිරිස් මල් දත්ත කට්ටලය හෝ ෆිෂර්ගේ අයිරිස් දත්ත කට්ටලය යනු බ්රිතාන්ය සංඛ්යාලේඛනඥයෙකු සහ ජීව විද්යාඥයෙකු වන රොනල්ඩ් ෆිෂර් විසින් 1936 දී ඔහුගේ 1936 පත්රිකාවේ භාවිතා කර ප්රසිද්ධියට පත් කරන ලද බහුවිචල්ය දත්ත සමූහයකි . [1] එය සමහර විට ඇන්ඩර්සන්ගේ අයිරිස් දත්ත කට්ටලය ලෙස හඳුන්වනු ලබන්නේ එඩ්ගා ඇන්ඩර්සන් විසින් අදාළ විශේෂ තුනක අයිරිස් මල් වල රූප විද්යාත්මක විචලනය ගණනය කිරීමට දත්ත රැස් කළ බැවිනි. [2] විශේෂ තුනෙන් දෙකක් ගස්පේ අර්ධද්වීපයේ "සියල්ලම එකම තණබිම් වලින් එකතු කරන ලද අතර, එකම දිනක නෙළා එකම උපකරණයක් ඇති එකම පුද්ගලයා විසින් එකම වේලාවක මනිනු ලැබේ". [3]
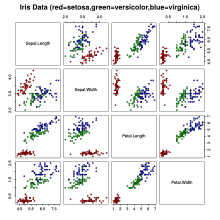
දත්ත කට්ටලය Iris විශේෂ තුනෙන් ( Iris setosa, Iris virginica සහ Iris versicolor ) සාම්පල 50කින් සමන්විත වේ. එක් එක් සාම්පලයෙන් ලක්ෂණ හතරක් මනිනු ලැබේ: සීපල් සහ පෙති වල දිග සහ පළල, සෙන්ටිමීටර වලින්. මෙම ලක්ෂණ හතරේ එකතුව මත පදනම්ව, ෆිෂර් විසින් විශේෂයන් එකිනෙකින් වෙන්කර හඳුනා ගැනීම සඳහා රේඛීය වෙනස්කම් කිරීමේ ආකෘතියක් නිර්මාණය කරන ලදී. ෆිෂර්ගේ පත්රිකාව Anals of Eugenics හි ප්රකාශයට පත් කරන ලද අතර phrenology ක්ෂේත්රයට අන්තර්ගත තාක්ෂණික ක්රම පිළිබඳ සාකච්ඡාව ඇතුළත් වේ. [1]


ෆිෂර්ගේ රේඛීය වෙනස්කම් විශ්ලේෂණය යෙදූ උදාහරණ දත්ත කට්ටලයක් ලෙස මුලින් භාවිතා කරන ලදී, එය ආධාරක දෛශික යන්ත්ර වැනි යන්ත්ර ඉගෙනීමේ බොහෝ සංඛ්යාන වර්ගීකරණ ශිල්පීය ක්රම සඳහා සාමාන්ය පරීක්ෂණ අවස්ථාවක් බවට පත්විය. [5]
කෙසේ වෙතත්, පොකුරු විශ්ලේෂණයේදී මෙම දත්ත කට්ටලය භාවිතා කිරීම සාමාන්ය දෙයක් නොවේ, මන්ද දත්ත කට්ටලය තුළ ඇත්තේ තරමක් පැහැදිලි වෙන්වීමක් සහිත පොකුරු දෙකක් පමණි. එක් පොකුරක Iris setosa අඩංගු වන අතර අනෙක් පොකුරේ Iris virginica සහ Iris versicolor යන දෙකම අඩංගු වන අතර Fisher භාවිතා කරන විශේෂ තොරතුරු නොමැතිව වෙන් කළ නොහැක. දත්ත කැණීමේදී අධීක්ෂණය කළ සහ අධීක්ෂණය නොකළ ශිල්පීය ක්රම අතර වෙනස පැහැදිලි කිරීමට දත්ත හොඳ ආදර්ශයක් සපයයි: ෆිෂර්ගේ රේඛීය වෙනස්කම් කිරීමේ ආකෘතිය ලබා ගත හැක්කේ වස්තු විශේෂ දන්නා විට පමණි: පන්ති ලේබල් සහ පොකුරු අනිවාර්යයෙන්ම සමාන නොවේ. [6]
එසේ වුවද, රේඛීය නොවන සහ අතු බෙදී යන ප්රධාන සංරචකය මත ප්රක්ෂේපණයේදී Iris විශේෂ තුනම වෙන් කළ හැකිය. [7] දත්ත කට්ටලය ආසන්නතම ගසකින් ආසන්න වශයෙන් නෝඩ් ගණන, නැමීම සහ දිගු කිරීම සඳහා යම් දඬුවමක් ඇත. එවිට ඊනියා "මෙට්රෝ සිතියම" ඉදිකරනු ලැබේ. [4] දත්ත ලක්ෂ්ය ආසන්නතම නෝඩයට ප්රක්ෂේපණය කෙරේ. එක් එක් නෝඩ් සඳහා ප්රක්ෂේපිත ලක්ෂ්යවල පයි රූප සටහන සකස් කර ඇත. පයි ප්රදේශය ප්රක්ෂේපිත ලක්ෂ්ය ගණනට සමානුපාතික වේ. විවිධ අයිරිස් විශේෂවල සාම්පලවල නිරපේක්ෂ බහුතරය විවිධ නෝඩ් වලට අයත් බව රූප සටහනෙන් (වමේ) පැහැදිලිය. Iris-virginica හි කුඩා කොටසක් පමණක් Iris-versicolor (රූප සටහනේ මිශ්ර නිල්-කොළ නෝඩ්) සමඟ මිශ්ර කර ඇත. එබැවින්, Iris විශේෂ තුන ( Iris setosa, Iris virginica සහ Iris versicolor ) රේඛීය නොවන ප්රධාන සංරචක විශ්ලේෂණයේ අධීක්ෂණ ක්රියා පටිපාටි මගින් වෙන් කළ හැකිය. ඒවා වෙනස් කොට සැලකීමට, ප්රධාන ගසෙහි අනුරූප නෝඩ් තෝරා ගැනීම පමණක් ප්රමාණවත් වේ.




| Dataset order | Sepal length | Sepal width | Petal length | Petal width | Species |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | I. setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | I. setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | I. setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | I. setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.3 | I. setosa |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 | I. setosa |
| 7 | 4.6 | 3.4 | 1.4 | 0.3 | I. setosa |
| 8 | 5.0 | 3.4 | 1.5 | 0.2 | I. setosa |
| 9 | 4.4 | 2.9 | 1.4 | 0.2 | I. setosa |
| 10 | 4.9 | 3.1 | 1.5 | 0.1 | I. setosa |
| 11 | 5.4 | 3.7 | 1.5 | 0.2 | I. setosa |
| 12 | 4.8 | 3.4 | 1.6 | 0.2 | I. setosa |
| 13 | 4.8 | 3.0 | 1.4 | 0.1 | I. setosa |
| 14 | 4.3 | 3.0 | 1.1 | 0.1 | I. setosa |
| 15 | 5.8 | 4.0 | 1.2 | 0.2 | I. setosa |
| 16 | 5.7 | 4.4 | 1.5 | 0.4 | I. setosa |
| 17 | 5.4 | 3.9 | 1.3 | 0.4 | I. setosa |
| 18 | 5.1 | 3.5 | 1.4 | 0.3 | I. setosa |
| 19 | 5.7 | 3.8 | 1.7 | 0.3 | I. setosa |
| 20 | 5.1 | 3.8 | 1.5 | 0.3 | I. setosa |
| 21 | 5.4 | 3.4 | 1.7 | 0.2 | I. setosa |
| 22 | 5.1 | 3.7 | 1.5 | 0.4 | I. setosa |
| 23 | 4.6 | 3.6 | 1.0 | 0.2 | I. setosa |
| 24 | 5.1 | 3.3 | 1.7 | 0.5 | I. setosa |
| 25 | 4.8 | 3.4 | 1.9 | 0.2 | I. setosa |
| 26 | 5.0 | 3.0 | 1.6 | 0.2 | I. setosa |
| 27 | 5.0 | 3.4 | 1.6 | 0.4 | I. setosa |
| 28 | 5.2 | 3.5 | 1.5 | 0.2 | I. setosa |
| 29 | 5.2 | 3.4 | 1.4 | 0.2 | I. setosa |
| 30 | 4.7 | 3.2 | 1.6 | 0.2 | I. setosa |
| 31 | 4.8 | 3.1 | 1.6 | 0.2 | I. setosa |
| 32 | 5.4 | 3.4 | 1.5 | 0.4 | I. setosa |
| 33 | 5.2 | 4.1 | 1.5 | 0.1 | I. setosa |
| 34 | 5.5 | 4.2 | 1.4 | 0.2 | I. setosa |
| 35 | 4.9 | 3.1 | 1.5 | 0.2 | I. setosa |
| 36 | 5.0 | 3.2 | 1.2 | 0.2 | I. setosa |
| 37 | 5.5 | 3.5 | 1.3 | 0.2 | I. setosa |
| 38 | 4.9 | 3.6 | 1.4 | 0.1 | I. setosa |
| 39 | 4.4 | 3.0 | 1.3 | 0.2 | I. setosa |
| 40 | 5.1 | 3.4 | 1.5 | 0.2 | I. setosa |
| 41 | 5.0 | 3.5 | 1.3 | 0.3 | I. setosa |
| 42 | 4.5 | 2.3 | 1.3 | 0.3 | I. setosa |
| 43 | 4.4 | 3.2 | 1.3 | 0.2 | I. setosa |
| 44 | 5.0 | 3.5 | 1.6 | 0.6 | I. setosa |
| 45 | 5.1 | 3.8 | 1.9 | 0.4 | I. setosa |
| 46 | 4.8 | 3.0 | 1.4 | 0.3 | I. setosa |
| 47 | 5.1 | 3.8 | 1.6 | 0.2 | I. setosa |
| 48 | 4.6 | 3.2 | 1.4 | 0.2 | I. setosa |
| 49 | 5.3 | 3.7 | 1.5 | 0.2 | I. setosa |
| 50 | 5.0 | 3.3 | 1.4 | 0.2 | I. setosa |
| 51 | 7.0 | 3.2 | 4.7 | 1.4 | I. versicolor |
| 52 | 6.4 | 3.2 | 4.5 | 1.5 | I. versicolor |
| 53 | 6.9 | 3.1 | 4.9 | 1.5 | I. versicolor |
| 54 | 5.5 | 2.3 | 4.0 | 1.3 | I. versicolor |
| 55 | 6.5 | 2.8 | 4.6 | 1.5 | I. versicolor |
| 56 | 5.7 | 2.8 | 4.5 | 1.3 | I. versicolor |
| 57 | 6.3 | 3.3 | 4.7 | 1.6 | I. versicolor |
| 58 | 4.9 | 2.4 | 3.3 | 1.0 | I. versicolor |
| 59 | 6.6 | 2.9 | 4.6 | 1.3 | I. versicolor |
| 60 | 5.2 | 2.7 | 3.9 | 1.4 | I. versicolor |
| 61 | 5.0 | 2.0 | 3.5 | 1.0 | I. versicolor |
| 62 | 5.9 | 3.0 | 4.2 | 1.5 | I. versicolor |
| 63 | 6.0 | 2.2 | 4.0 | 1.0 | I. versicolor |
| 64 | 6.1 | 2.9 | 4.7 | 1.4 | I. versicolor |
| 65 | 5.6 | 2.9 | 3.6 | 1.3 | I. versicolor |
| 66 | 6.7 | 3.1 | 4.4 | 1.4 | I. versicolor |
| 67 | 5.6 | 3.0 | 4.5 | 1.5 | I. versicolor |
| 68 | 5.8 | 2.7 | 4.1 | 1.0 | I. versicolor |
| 69 | 6.2 | 2.2 | 4.5 | 1.5 | I. versicolor |
| 70 | 5.6 | 2.5 | 3.9 | 1.1 | I. versicolor |
| 71 | 5.9 | 3.2 | 4.8 | 1.8 | I. versicolor |
| 72 | 6.1 | 2.8 | 4.0 | 1.3 | I. versicolor |
| 73 | 6.3 | 2.5 | 4.9 | 1.5 | I. versicolor |
| 74 | 6.1 | 2.8 | 4.7 | 1.2 | I. versicolor |
| 75 | 6.4 | 2.9 | 4.3 | 1.3 | I. versicolor |
| 76 | 6.6 | 3.0 | 4.4 | 1.4 | I. versicolor |
| 77 | 6.8 | 2.8 | 4.8 | 1.4 | I. versicolor |
| 78 | 6.7 | 3.0 | 5.0 | 1.7 | I. versicolor |
| 79 | 6.0 | 2.9 | 4.5 | 1.5 | I. versicolor |
| 80 | 5.7 | 2.6 | 3.5 | 1.0 | I. versicolor |
| 81 | 5.5 | 2.4 | 3.8 | 1.1 | I. versicolor |
| 82 | 5.5 | 2.4 | 3.7 | 1.0 | I. versicolor |
| 83 | 5.8 | 2.7 | 3.9 | 1.2 | I. versicolor |
| 84 | 6.0 | 2.7 | 5.1 | 1.6 | I. versicolor |
| 85 | 5.4 | 3.0 | 4.5 | 1.5 | I. versicolor |
| 86 | 6.0 | 3.4 | 4.5 | 1.6 | I. versicolor |
| 87 | 6.7 | 3.1 | 4.7 | 1.5 | I. versicolor |
| 88 | 6.3 | 2.3 | 4.4 | 1.3 | I. versicolor |
| 89 | 5.6 | 3.0 | 4.1 | 1.3 | I. versicolor |
| 90 | 5.5 | 2.5 | 4.0 | 1.3 | I. versicolor |
| 91 | 5.5 | 2.6 | 4.4 | 1.2 | I. versicolor |
| 92 | 6.1 | 3.0 | 4.6 | 1.4 | I. versicolor |
| 93 | 5.8 | 2.6 | 4.0 | 1.2 | I. versicolor |
| 94 | 5.0 | 2.3 | 3.3 | 1.0 | I. versicolor |
| 95 | 5.6 | 2.7 | 4.2 | 1.3 | I. versicolor |
| 96 | 5.7 | 3.0 | 4.2 | 1.2 | I. versicolor |
| 97 | 5.7 | 2.9 | 4.2 | 1.3 | I. versicolor |
| 98 | 6.2 | 2.9 | 4.3 | 1.3 | I. versicolor |
| 99 | 5.1 | 2.5 | 3.0 | 1.1 | I. versicolor |
| 100 | 5.7 | 2.8 | 4.1 | 1.3 | I. versicolor |
| 101 | 6.3 | 3.3 | 6.0 | 2.5 | I. virginica |
| 102 | 5.8 | 2.7 | 5.1 | 1.9 | I. virginica |
| 103 | 7.1 | 3.0 | 5.9 | 2.1 | I. virginica |
| 104 | 6.3 | 2.9 | 5.6 | 1.8 | I. virginica |
| 105 | 6.5 | 3.0 | 5.8 | 2.2 | I. virginica |
| 106 | 7.6 | 3.0 | 6.6 | 2.1 | I. virginica |
| 107 | 4.9 | 2.5 | 4.5 | 1.7 | I. virginica |
| 108 | 7.3 | 2.9 | 6.3 | 1.8 | I. virginica |
| 109 | 6.7 | 2.5 | 5.8 | 1.8 | I. virginica |
| 110 | 7.2 | 3.6 | 6.1 | 2.5 | I. virginica |
| 111 | 6.5 | 3.2 | 5.1 | 2.0 | I. virginica |
| 112 | 6.4 | 2.7 | 5.3 | 1.9 | I. virginica |
| 113 | 6.8 | 3.0 | 5.5 | 2.1 | I. virginica |
| 114 | 5.7 | 2.5 | 5.0 | 2.0 | I. virginica |
| 115 | 5.8 | 2.8 | 5.1 | 2.4 | I. virginica |
| 116 | 6.4 | 3.2 | 5.3 | 2.3 | I. virginica |
| 117 | 6.5 | 3.0 | 5.5 | 1.8 | I. virginica |
| 118 | 7.7 | 3.8 | 6.7 | 2.2 | I. virginica |
| 119 | 7.7 | 2.6 | 6.9 | 2.3 | I. virginica |
| 120 | 6.0 | 2.2 | 5.0 | 1.5 | I. virginica |
| 121 | 6.9 | 3.2 | 5.7 | 2.3 | I. virginica |
| 122 | 5.6 | 2.8 | 4.9 | 2.0 | I. virginica |
| 123 | 7.7 | 2.8 | 6.7 | 2.0 | I. virginica |
| 124 | 6.3 | 2.7 | 4.9 | 1.8 | I. virginica |
| 125 | 6.7 | 3.3 | 5.7 | 2.1 | I. virginica |
| 126 | 7.2 | 3.2 | 6.0 | 1.8 | I. virginica |
| 127 | 6.2 | 2.8 | 4.8 | 1.8 | I. virginica |
| 128 | 6.1 | 3.0 | 4.9 | 1.8 | I. virginica |
| 129 | 6.4 | 2.8 | 5.6 | 2.1 | I. virginica |
| 130 | 7.2 | 3.0 | 5.8 | 1.6 | I. virginica |
| 131 | 7.4 | 2.8 | 6.1 | 1.9 | I. virginica |
| 132 | 7.9 | 3.8 | 6.4 | 2.0 | I. virginica |
| 133 | 6.4 | 2.8 | 5.6 | 2.2 | I. virginica |
| 134 | 6.3 | 2.8 | 5.1 | 1.5 | I. virginica |
| 135 | 6.1 | 2.6 | 5.6 | 1.4 | I. virginica |
| 136 | 7.7 | 3.0 | 6.1 | 2.3 | I. virginica |
| 137 | 6.3 | 3.4 | 5.6 | 2.4 | I. virginica |
| 138 | 6.4 | 3.1 | 5.5 | 1.8 | I. virginica |
| 139 | 6.0 | 3.0 | 4.8 | 1.8 | I. virginica |
| 140 | 6.9 | 3.1 | 5.4 | 2.1 | I. virginica |
| 141 | 6.7 | 3.1 | 5.6 | 2.4 | I. virginica |
| 142 | 6.9 | 3.1 | 5.1 | 2.3 | I. virginica |
| 143 | 5.8 | 2.7 | 5.1 | 1.9 | I. virginica |
| 144 | 6.8 | 3.2 | 5.9 | 2.3 | I. virginica |
| 145 | 6.7 | 3.3 | 5.7 | 2.5 | I. virginica |
| 146 | 6.7 | 3.0 | 5.2 | 2.3 | I. virginica |
| 147 | 6.3 | 2.5 | 5.0 | 1.9 | I. virginica |
| 148 | 6.5 | 3.0 | 5.2 | 2.0 | I. virginica |
| 149 | 6.2 | 3.4 | 5.4 | 2.3 | I. virginica |
| 150 | 5.9 | 3.0 | 5.1 | 1.8 | I. virginica |
යන්ත්ර ඉගෙනීමේ අරමුණු සඳහා ආරම්භක දත්ත කට්ටලයක් ලෙස අයිරිස් දත්ත කට්ටලය බහුලව භාවිතා වේ. දත්ත කට්ටලය R පාදයේ සහ Python යන්ත්ර ඉගෙනුම් පුස්තකාලයේ Sikit-Learn හි ඇතුළත් කර ඇත, එවිට පරිශීලකයින්ට ඒ සඳහා මූලාශ්රයක් සොයා නොගෙන ප්රවේශ විය හැක.
දත්ත කට්ටලයේ අනුවාද කිහිපයක් ප්රකාශයට පත් කර ඇත. [8]
R කේතය භාවිතය නිදර්ශනය කරයි
සංස්කරණය# Show the dataset
iris
# Show the help page, with information about the dataset
?iris
# Create scatterplots of all pairwise combination of the 4 variables in the dataset
pairs(iris[1:4], main="Iris Data (red=setosa,green=versicolor,blue=virginica)",
pch=21, bg=c("red","green3","blue")[unclass(iris$Species)])
from sklearn.datasets import load_iris
iris = load_iris()
iris
මෙම කේතය ලබා දෙන්නේ:
{'data': array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3., 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],...
'target': array([0, 0, 0, ... 1, 1, 1, ... 2, 2, 2, ...
'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),
...}
- සම්භාව්ය දත්ත කට්ටල
- යන්ත්ර ඉගෙනුම් පර්යේෂණ සඳහා දත්ත කට්ටල ලැයිස්තුව
යොමු කිරීම්
සංස්කරණය- ^ a b R. A. Fisher (1936). "The use of multiple measurements in taxonomic problems". Annals of Eugenics. 7 (2): 179–188. doi:10.1111/j.1469-1809.1936.tb02137.x.
{{cite journal}}:|hdl-access=requires|hdl=(help) උපුටාදැක්වීම් දෝෂය: Invalid<ref>tag; name "fisher36" defined multiple times with different content - ^ Edgar Anderson (1936). "The species problem in Iris". Annals of the Missouri Botanical Garden. 23 (3): 457–509. doi:10.2307/2394164. JSTOR 2394164.
- ^ Edgar Anderson (1935). "The irises of the Gaspé Peninsula". Bulletin of the American Iris Society. 59: 2–5.
- ^ a b A. N. Gorban, A. Zinovyev. Principal manifolds and graphs in practice: from molecular biology to dynamical systems, International Journal of Neural Systems, Vol. 20, No. 3 (2010) 219–232.
- ^ "UCI Machine Learning Repository: Iris Data Set". archive.ics.uci.edu. සම්ප්රවේශය 2017-12-01.
- ^ Ines Färber, Stephan Günnemann, Hans-Peter Kriegel, Peer Kröger, Emmanuel Müller, Erich Schubert, Thomas Seidl, Arthur Zimek (2010). "On Using Class-Labels in Evaluation of Clusterings".
- ^ A.N. Gorban, N.R. Sumner, and A.Y. Zinovyev, Topological grammars for data approximation, Applied Mathematics Letters Volume 20, Issue 4 (2007), 382-386.
- ^ Bezdek, J.C. and Keller, J.M. and Krishnapuram, R. and Kuncheva, L.I. and Pal, N.R. (1999). "Will the real iris data please stand up?". IEEE Transactions on Fuzzy Systems. 7: 368–369. doi:10.1109/91.771092.
{{cite journal}}: CS1 maint: multiple names: authors list (link)
බාහිර සබැඳි
සංස්කරණය- "Fisher's Iris Data". (Contains two errors which are documented). UCI Machine Learning Repository: Iris Data Set.