1 − 2 + 3 −4...

1 − 2 + 3 − 4 + • • • ගණිතයේදි 1-2+3-4+...යනු පද, අනුයාත ධන නිඛිල වන, ලකුණු ප්‍රත්‍යාවර්ත ලෙස යොදා ගන්නා අපිරිමිත ශ්‍රේණියයි. සිග්මා සමාකලන අංකනය යොදාගනිමින් ශ්‍රේණියේ පළමු m පද වල ඓක්‍යය පහත ලෙස දැක්විය හැක.

$\sum _{n=1}^{m}n(-1)^{n-1}.$

අපිරිමිත ශ්‍රේණිය අපසාරී වේ. එනම් එහි ආංශික ඓක්‍යය (1,-1,2,-2,...) නියත අන්තයක් කරා ළගා නොවේ. කෙසේ නමුත් 18වන ශතවර්ෂයේදී ලියොනාර්ඩ් යූලර් විසින් තේරුම් ගැනීම දුෂ්කර බවට ඔහු පිළිගත් සමීකරණයක් ඉදිරිපත් කරන ලදී.

$1-2+3-4+\cdots ={\frac {1}{4}}.$

මෙම සමීකරණය සඳහා පිළිගත හැකි විවරණයක් බොහෝ කලක් යන තුරු ඉදිරිපත් නොවුණි. 1890 පටන් අර්නස්ටෝ සෙසාරෝ, එමිලි බොරෙල් ආදී පිරිසක් යූලර්ගේ සමීකරණයට නව අර්ථකථන ඇතුළු අපසාරී ශ්‍රේණි වලට සාධාරික ඓක්‍යයන් දිය හැකි ක්‍රම පිළිබඳ පරීක්ෂණ සිදු කළහ.මෙම ක්‍රම බොහොමයකින් අවසානයේදී 1-2+3-4+... සඳහා 1/4 ක ඓක්‍යයක් ලැබුණි. සෙසාරෝ සමාකලනය යනු 1-2+3-4... සඳහා ඓක්‍යයක් ලබා නොදෙන ක්‍රම කිහිපයෙන් එකකි. එනම් එය අබෙල් සමාකලනය වැනි තරමක් ප්‍රබල ක්‍රමයක් අවශ්‍ය වන අවස්ථාවකට උදාහරණයකි. 1-2+3-4+... ශ්‍රේණිය 1-1+1-1+... යන ග්‍රැන්ඩිගේ ශ්‍රේණියට බොහෝ සමානතා දක්වයි. යූලර් විසින් 1-2n+3n-4n+…. (ඕනැම n අගයක් සඳහා) හි විශේෂ අවස්ථා ලෙස ඉහත ශ්‍රේණි සලකමින් ඔහුගේ බේසල් ගැටළුව Dirichlet eta ශ්‍රිතය හා Riemann zeta ශ්‍රිතය ලෙස අද හඳුන්වන ශ්‍රිතීය සමීකරණ දක්වා ගෙන යාමට සමත් විය. අපසාරීතාව ශ්‍රේණියේ පද (1,-2,3,-4...) ශුන්‍යයට ළඟා නොවේ. එබැවින් 1-2+3-4+... අපසාරී වේ. අපසාරීතාව පිළිබඳ මූලික දැනුමක් තිබීම පසුව වැදගත් වේ. නිර්වචනයට අනුව, ශ්‍රේණියක අභිසාරීතාව හෝ අපසාරීතාව නිශ්චය කරනු ලබන්නේ එහි ආංශික ඓක්‍යයන්හි අනුක්‍රමයේ අභිසාරීතාව හෝ අපසාරීතාව අනුවය. 1-2+3-4+... හි ආංශික ඓක්‍යයන් වනුයේ

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

...

මෙම අනුක්‍රමයේදී සියළු නිඛිල එක් වරක් හමු වෙන අතර--ශුන්‍ය ආංශික ඓක්‍ය සැලකූ විට 0 ද ඇතුලත් වේ-- එමඟින් z නිඛිල කුලකයෙහි ගණ්‍යතාවය තහවුරු කරයි. ආංශික ඓක්‍යයන්ගේ අනුක්‍රමය මෙම ශ්‍රිතය එක් නිශ්චිත සංඛ්‍යාවක් වෙත අභිසාරී නොවන බව පැහැදිලි කරයි ( ඕනැම x සීමාවක් සඳහා ආංශික ඓක්‍යයන් [x-1, x+1] පරාසයෙන් පිටත පිහිටන ලක්ෂ්‍යයක් ඇත ). එනම් 1-2+3-4+...අපසාරී වේ.

සමාකලනය සඳහා ස්වතෝන්වේෂණ ක්‍රම

ස්ථායීතාව හා රේඛීයතාව

1,-2,3,-4,5,-6....සරල රටාවක් අනුගමනය කරන බැවින් 1-2+3-4+.... යන ශ්‍රේණියේ පද එකතු කිරීමෙන් සංඛ්‍යාත්මක අගයක් ලබා ගතහැකි වේ. යම් S සංඛ්‍යාවක් සඳහා s=1-2+3-4+...නම් පහත ගණනයෙන් S=1/4 බව පෙන්වයි.

${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$

එනම් $s={\frac {1}{4}}$. මෙම ව්‍යුත්පන්නය දකුණුපස ප්‍රස්තාරයෙන් දක්වා ඇත.

1-2+3-4+....සඳහා ඓක්‍යයක් නොමැති ලෙස සලකන නමුත්, ඓක්‍යයක් දැක්වීමට අවශ්‍ය වුවහොත් S=1-2+3-4+...=1/4 යනු ඒ සඳහා යොදා ගත හැකි සුදුසුම සමීකරණය වේ. අපසාරී ශ්‍රේණියක ඓක්‍යය සඳහා නිර්වචනයක් ලෙස සමාකලන ක්‍රමය සැලකිය හැක. මෙහිදී සියලුම ශ්‍රේණිවල ඇතැම් උපකුලකයන්හි ඓක්‍යය සලකනු ලබයි. මේ සඳහා භාවිතා කළ හැකි තවත් ක්‍රම ඇති අතර ඒවායෙහි හා සාමන්‍ය සමාකලනයෙහි ලක්ෂණ අතර ඇති සමානතා අනුව ඒවා විවිධ වේ. ඉහත ගණනයෙන් සාධනය කරනු ලබන්නේ; 1-2+3-4+...ශ්‍රේණියට ඓක්‍යයක් දිය හැකි ඕනෑම රේඛීය හා ස්ථායී සමාකලන ක්‍රමයකින් ලබාදෙන ඓක්‍යය ¼ වන බවය. එසේම,

${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+&(-2+3-4+\cdots )&{}+1-2&+(3-4+5\cdots )\\&=&0+&(-2+3)+(3-4)+(-4+5)+\cdots \\2s&=&&1-1+1-1\cdots \end{array}}$

වන බැවින් මෙම ක්‍රමය ග්‍රැන්ඩිගේ ශ්‍රේණියටද පහත ලෙස අගයක් ලබා දෙයි. 1-1+1-1+..=1/2

කෞචි ගුණිතය

1891 දී අර්නස්ටෝ සෙසාරෝ අපසාරී ශ්‍රේණි , කලනය මඟින් පැහැදිලි කිරීමට සමත් විය. (1-1+1-1+...)2=1-2+3-4+... වන බව හා දෙපසම 1/4ට සමාන වන බව ඔහු පෙන්වා දෙන ලදී. මෙම සමීකරණය සෙසාරෝ විසින් මීට පෙර වසරේ දී ඉදිරිපත් කරන ලද, ඓක්‍යයක් ලබා ගත හැකි අපසාරී ශ්‍රේණි පිළිබඳ වූ ප්‍රථම නියමයෙහි යෙදීමක් ලෙස සැලකිය හැක. ඔහුගේ සමාකලන නියමයට අනුව 1-1+1-1+... හා 1-1+1-1+.... හී කෞචි ගුණිතය 1-2+3-4+.... වේ. අපරිමිත ශ්‍රේණි දෙකක කෞචි ගුණිතය නිර්වචනය කිරීම සඳහා ශ්‍රේණි දෙකම අපසාරී විය යුතුය.

${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$

එවිට ශ්‍රේණිය වනුයේ

$\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .$

එසේම කෞචි ගුණිතය අනුව 1-1+1-1+...=1/2 ලෙස ලබා දෙන සමාකලන ක්‍රමයක් 1-2+3-4=1/4 ලෙසද ඓක්‍යක් ලබා දෙයි. ඉහත ප්‍රතිඵලය අනුව 1-1+1-1+... සහ 1-2+3-4+... හි සමාකලනයේ තුල්‍යතාව රේඛීය, ස්ථායී හා කෞචි ගුණිතයට අදාළ ක්‍රම මඟින් පෙන්නුම් කරයි. සෙසාරෝගේ නියමය මීට උදාහරණයකි. 1-1+1-1+.... ශ්‍රේණිය දුර්වල ලෙස සෙසාරෝ සමාකල්‍ය වේ. එය (c, 1) සමාකල්‍ය ලෙස හැඳින්වේ. 1-2+3-4+... සෙසාරෝ සමාකල්‍යයේ ප්‍රබල අවස්ථාවක් වන අතර එය (c, 2) සමාකල්‍යය ලෙස හැඳින්වේ. සෙසාරෝ නියමයේ සියලු අවස්ථා රේඛීය හා ස්ථායී වන බැවින් ගණනය කරන ලද ඓක්‍යයන් ඒ ආකාර වේ.

නිර්දිශ්ට ක්‍රම සෙසාරෝ සහ හෝල්ඩර්

Data about the (H, 2) sum of ​¹⁄₄

පවත්නාවූ 1-2+3-4+...හි (c,1) සෙසාරෝ ඓක්‍යය පෙන්වීම සඳහා, ශ්‍රේණියේ ඓක්‍යයන්හි මධ්‍යයනය ගණනය කිරීම අවශ්‍ය වේ. ආංශික ඓක්‍යයන් වනුයේ: 1,-1,2,-2,3,-3,....... හා මධ්‍යයන වනුයේ: 1, 0, 2/3, 0, 3/5, 0, 4/7,..... මෙම මධ්‍යයන අනුක්‍රමය අභිසාරී නොවේ. එබැවින් 1-2+3-4+...... සෙසාරෝ සමාකල්‍ය නොවේ. සෙසාරෝ සමාකලනය සඳහා පිළිගත් ව්‍යාප්තිකරණ දෙකකි. වඩා සරල වනුයේ, n ප්‍රකෘති සංඛ්‍යා සඳහා වන (H, n) අනුක්‍රමයයි. (H, n) ඓක්‍යය සෙසාරෝ සමාකල්‍ය වන අතර අනෙක් සංකීර්ණ ක්‍රම මධ්‍යයනය ගණනය කරයි. ඉහත ක්‍රමයේ, ඉරට්ටේ සංඛ්‍යාවල මධ්‍යයනය 1/2 වන අතර ඔත්තේ සංඛ්‍යාවල මධ්‍යයනය 0ට සමාන වේ. එබැවින් මධ්‍යයනයන්හි මධ්‍යයනය 0 හා 1/2 හි සාමාන්‍යය වෙත අභිසාරී වේ. එනම් 1-2+3-4+..., 1/4 ට (H, n) සමාකල්‍ය වේ. H මඟින් “ඔටෝ හෝල්ඩර්” සංකේතවත් වේ. ඔහු 1882 දී පළමු වරට අබෙල් සමාකලනය හා (H,n ) සමාකලනයේ සම්බන්ධය පෙන්වා දෙන ලදී. 1-2+3-4+...ඔහුගේ ප්‍රථම උදාහරණයයි. 1/4 යනු 1-2+3-4+...හි (H, 2) සමාකලනය වීම, එය අබෙල් සමාකලනය බව තහවුරු කරයි. මෙය පහත සාධනය කර ඇත. අනෙක් පිළිගත් සෙසාරෝ සමාකලනයෙහි ව්‍යාප්තිකරණය වනුයේ (C,n ) අනුක්‍රමයයි. (C,n ) සමාකලනයේ හා (H,n ) සමාකලනයේ අගය සමාන බව ඔප්පු කර ඇති නමුදු ඓතිහාසික පදනම වෙනස් වේ. 1887 දී සෙසාරෝ (C, n) සමාකලනයේ නිර්වචනය දැක්වීමට සමත් වුවද ඔහුට ඉදිරිපත් කළ හැකි වූයේ සුළු උදාහරණ ප්‍රමාණයකි. 1-2+3-4+... හි ඓක්‍යය 1/4 ලෙස ඔහු (C, n) වැනි ක්‍රමයකින් ගණනය කළද එය නිවැරදි ලෙස සාධනය කිරීමට ඔහු අසමත් විය. ඔහු 1890දී (C,n ) ක්‍රම නිර්වචනය කරමින් ඔහුගේ නියමය ඉදිරිපත් කළේය. එනම් (C, n) සමාකල්‍ය ශ්‍රේණියක හා (C,m ) සමාකල්‍ය ශ්‍රේණියක කෞචි ගුණිතය (C, m+n+1) සමාකල්‍ය වන බවයි.

අබෙල් සමාකලනය 1749දී ශ්‍රේණියක් අපසාරී වන නමුත් ඓක්‍යයක්ද ලබා දෙන බව ලියොනාර්ඩ් යුලර් සඳහන් කරන ලදී. 1-2+3-4+5-6..හි ඓක්‍යය 1/4 යන්න පරස්පර විරෝධී වේ. මෙම ශ්‍රේණියේ පද 100ක එකතුව -50 වන අතර පද 101ක් වූ විට ඓක්‍යය +51 වේ. එය 1/4ට හාත්පසින් වෙනස් වන අතර පද සංඛ්‍යාව වැඩි වත්ම ඓක්‍යයද වැඩි වේ. නමුත් 'ඓක්‍යය' යන්නට මෙහිදී වඩා පුළුල් අර්ථයක් අවශ්‍ය වේ.... යුලර් විසින් 'ඓක්‍යය' යන්නට අර්ථ දැක්වීම් කිහිපයක් ලබා දී ඇත. 1-2+3-4+....යන අවස්ථාවේදී ඔහුගේ පැහැදිලි කිරීම් අබෙල් සමාකලනයට බෙහෙවින් සමාන වේ. 1-2+3-4+5..ශ්‍රේණිය 1/(1+1)2 යන සූත්‍රයේ ප්‍රසාරණය වන බැවින් ශ්‍රේණියේ ඓක්‍යය ද සූත්‍රයේ අගය වන 1/4 වන බව නිසැකය. 1/(1+x)2 යන ප්‍රකාශනය ප්‍රසාරණය කිරීමෙන් ලබා ගන්නා 1-2x+3x2-4x3+5x4-6x5+…. ශ්‍රේණිය සලකා බැලීමෙන් මෙය වඩාත් පැහැදිලි වේ; x=1 වන විට මෙය ඉහත අවස්ථාවට සමාන වන බැවිනි. |x|<1 වන නියත අගයක් සඳහා, යුලර් නිවැරදි බව පෙන්වීමට බොහෝ උදාහරණ ඇත.

$1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.$

ප්‍රකාශනයේ දකුණුපස ටේලර් ප්‍රසාරණය හෝ බහුපද ප්‍රකාශන සඳහා සම්මත දීර්ඝ බෙදීමේ ක්‍රමය මෙහිදී සලකා බැලිය හැක. වම් පස පදය (1+x) න් දෙවරක් ගුණ කිරීමෙන් හෝ 1-2x+3x2-4x3+... යන ගුණෝත්තර ශ්‍රේණිය වර්ග කිරීමෙන් හෝ ඉහත ක්‍රම යෙදිය හැක. අපර ශ්‍රේණිය අවකලනය කිරීමද යුලර් විසින් යෝජනා කරන ලද ක්‍රමයකි. නව අදහසට අනුව x=1 වන විට 1-2x+3x2-4x3+... ශ්‍රේණිය ශ්‍රිතයක් ලබා නොදෙයි. එනම් ප්‍රකාශනයට එම අගය ආදේශ කළ නොහැක. මෙහිදී සියළු |x|<1 සඳහා ශ්‍රිතය නිර්වචනය කළ හැකි බැවින් x, 1ට ළඟාවන සීමාව සැලකීමට හැක. මෙය අබෙල් සමාකලනයේ නිර්වචනයයි.

$\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

යුලර් සහ බොරෙල්

Euler summation to ​¹⁄₂ − ​¹⁄₄

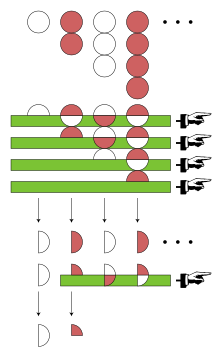
මෙම ශ්‍රේණිය සඳහා යුලර් තවත් ක්‍රමයක් ආදේශ කළේය. ඔහුගේ සොයාගැනීමක් වන එය යුලර් පරිණාමිතය ලෙස හැඳින්වේ. යුලර් පරිණාමිතය ගණනය කිරීම ප්‍රත්‍යාවර්තිත ශ්‍රේණියට අයත් ධන පද වලින් ආරම්භ කළ හැක- එය මෙහිදී 1,2,3,4,.... වේ. මෙම අනුක්‍රමයේ පළමු පදය a0 වේ. මීළඟට 1,2,3,4,... හි ඇති අභීප අන්තර අවශ්‍ය වේ. එනම් 1,1,1,1.... මෙම අනුක්‍රමයේ පළමු අගය ∆a0 යි. යුලර් පරිණාමිතය අන්තරයන්හි අන්තර හා පුනහ්කරණ මතද පදනම් වේ. නමුත් 1,1,1,1....අතර ඇති සියළු අභීප අන්තර 0 වේ. එබැවින් 1-2+3-4+...හි යුලර් පරිණාමිතය පහත ලෙස දැක්විය හැක.

${\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.$

නව නාමකරණයට අනුව, 1-2+3-4+...., 1/4ට යුලර් සමාකල්‍ය වේ.

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),$

1-2+3-4+.... ඉහත ලෙස දක්වමින් පහත අභිසාරී ශ්‍රේණිය ලබාගත හැක.

$a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).$

එබැවින් 1-2+3-4+.... හි බොරෙල් ඓක්‍යය වනුයේ,

$\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.$

පරිමාණ විභේදනය අත්‍යණුක විස්ථාපනය හා පරිමාණ විභේදනය යන භෞතික මූලධර්ම දෙක පමණක් භාවිතා කරමින් Saichev හා Woyczyński විසින් 1-2+3-4+...=1/4 බව පෙන්වා දීමට සමත් වූහ. ශ්‍රේණියේ ඓක්‍යය 1/4 ලෙස ලබා දෙන 'φ සමාකලන ක්‍රම' රාශියක් පැහැදිලි කිරීමට මෙම මූලධර්ම භාවිතා කළ හැක. φ(0)=1 හා +∞ හි දී φ(x) හා xφ(x) හි සීමා 0 වන විට, φ යනු පළමු හා දෙවන ව්‍යුත්පන්න (0, ∞) දී අඛණ්ඩ හා අනුකල්‍ය වන ශ්‍රිතයක් නම්,

$\lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.$

මෙය φ(x) = exp (-x) වන විට අබෙල් සමාකලනය පැහැදිලි කරයි. ශ්‍රේණියේ පද m වටා යුගලනය කිරීමෙන් සහ ප්‍රකාශනය රීමන් නිඛිලයක් බවට පරිවර්තනය කිරීමෙන් එය සාධනය කළ හැක. මීළඟ පියවර ලෙස 1-1+1-1+... හී සාධනය මධ්‍යයන අගය ප්‍රමේය යොදා ගනී. නමුත් මෙහිදී ඒ සඳහා ටේලර් ප්‍රමේයයේ ලාග්‍රාන්ජ් අවස්ථාව අවශ්‍ය වේ.

ව්‍යාප්තිකරණ 1-1+1-1+... හි තෙවැදෑරුම් කෞචි ගුණිතය වනුයේ 1-3+6-10+..., එනම් ත්‍රිකෝණික සංඛ්‍යාවල ප්‍රත්‍යාවර්තිත ශ්‍රේණියයි. එහි අබෙල් හා යුලර් සමාකලනය වනුයේ 1/8. 1-1+1-1+... හි චතුර්විධ කෞචි ගුණිතය 1-4+10-20+... වන අතර එය චතුස්තලීය සංඛ්‍යාවල ප්‍රත්‍යාවර්තිත ශ්‍රේණියයි. එහි අබෙල් ඓක්‍යය 1/16 වේ. 1-2+3-4+... හි තවත් ව්‍යාප්තිකරණයක් වනුයේ 1-2n+3n-4n+…. (අනෙක් n අගයන් සඳහා). n ධන නිඛිල සඳහා මෙම ශ්‍රේණිය පහත අබෙල් ඓක්‍යයන් ලබා දෙයි. Bn බනෝලි සංඛ්‍යා නම්, 1-2n+3n- ……. = ( 2^(n+1)-1)/(n+1) B_(n+1) ඉරට්ටේ n සංඛ්‍යා සඳහා මෙය පහත අයුරු වේ. 1-22k+32k-……. = 0

1826දී මෙම අවසාන ඓක්‍යය නීල්ස් හෙන්‍රික් අබෙල් ගේ විවේචනයට පාත්‍ර විය; "අපසාරී ශ්‍රේණි යනු යක්ෂයාගේ ක්‍රියාවකි. කිසිවෙක් ඒ සඳහා සාධනයක් ඉදිරිපත් කිරීම ලැජ්ජාවට කරුණකි. එය භාවිතා කිරීමෙන් තමාට අවශ්‍ය දෙය ලබා ගැනීමට හැක. එබැවින් එය බොහෝ අසතුටුදායක මෙන්ම පරස්පර විරෝධී අදහස් නිර්මාණය කර ඇත. කිසිවෙකුට හෝ 0 = 1-2n+3n-4n+… (n ධන නිඛිල වන විට ) යන සමීකරණයට වඩා දරුණු දෙයක් පිළිබඳ සිතා ගත හැකිද? මිතුරනි, මෙය සිනහවට කරුණකි ". සෙසාරෝ ගේ ගුරුවරයා වන ඉයුජින් චාර්ල්ස් කැටලන්ද අපසාරී ශ්‍රේණි විවේචනය කළේය. කැටලන්ගේ ආභාෂයෙන් සෙසාරෝ ද 1-2n+3n-4n+… සඳහා වන සූත්‍ර 'හාස්‍යජනක සමානතා' ලෙස හැඳින්වීය. 1883දී සෙසාරෝ විසින් මෙම සූත්‍ර නිවැරදි නොවන නමුත් ඇතැම් විට ප්‍රයෝජනවත් වන බවට අදහස් දැක්විය. නමුත් 1890දී ඔහුගේ Sur la multiplication des séries තුළින් නිර්වචන ඔස්සේ නව එළඹුමක් ලබා දීමට සමත් විය. මෙම ශ්‍රේණි නිඛිල නොවන n සංඛ්‍යා සඳහා ද අදාළ කර ගත හැක. එය Dirichlet eta ශ්‍රිතය ලබා දෙයි. 1-2+3-4+... ට අදාළ ශ්‍රිතයන් අධ්‍යයනය කිරීමට යුලර් උත්සුක වීමට තවත් හේතුවක් වූයේ ශ්‍රිතීය සමීකරණයි. එය සෘජුවම Riemann zeta ශ්‍රිතයට සම්බන්ධ වේ. යුලර් ඒ වනවිට ද ධන ඉරට්ටේ සංඛ්‍යා සඳහාමෙම ශ්‍රිතයන්ට අගයන් සොයාගෙන සිටි අතර(බේසල් ගැටළුවද ඇතුළුව ), ධන ඔත්තේ සංඛ්‍යා සඳහා ද ලැබෙන අගයන් සෙවීමට උත්සාහ දරමින් සිටියේය (ඇපෙරි නියතය ද ඇතුළුව ). වර්තමානයේදී මෙම ගැටළුව විසඳිය නොහැක්කක් ලෙස සලකනු ලබයි. Eta ශ්‍රිතයේ Dirichlet ශ්‍රේණිය සෑමතැන්හිදීම අබෙල් සමාකල්‍ය වන බැවින්, එය යුලර්ගේ ක්‍රමවේදයන් භාවිතා කරමින් විසඳීම පහසුවේ. නමුත් Zeta ශ්‍රිතයේ Dirichlet ශ්‍රේණිය අපසාරී වන අවස්ථාවේදී එහි ඓක්‍යය සෙවීම අපහසු වේ. උදා: 1+2+3+4+...යන ප්‍රත්‍යාවර්තිත ශ්‍රේණිය zeta ශ්‍රිතයේ 1-2+3-4+...හි පූරණයයි. එය නූතන භෞතික විද්‍යාවේදී බොහෝ සෙයින් භාවිතා වන නමුත් ඓක්‍යය සෙවීම සඳහා වඩා ප්‍රබල ක්‍රමවේද අවශ්‍ය වේ.