සමෝච්ච රේඛාව
විචල්ය දෙකක ශ්රිතයක සමෝච්ච රේඛාවක් (සමරේඛාවක්, විචල්යමූලකයක්, හෝ සමසංඛ්යා රේඛාවක් ලෙසින්ද හැඳින්වේ) යනු, එය ඔස්සේ ශ්රිතය නියත අගයක් දරන්නාවූ වක්රයකි.[1] සිතියම් විද්යාවේදී, සමෝච්ච රේඛාවක් (බොහෝවිට "සමෝච්චයක්" ලෙසින් හැඳින්වෙයි) විසින්, මධ්යන්යය මුහුදු මට්ටම වැනි දී ඇති මට්ටමකට උඩින් වූ සමාන උන්නතාංශයක් (උසක්) සහිත ලක්ෂ්යයන් එකට යා කරයි. [2] සමෝච්ච සිතියමක් යනු, සමෝච්ච රේඛා සන්නිදර්ශනය කරන සහ, නිදසුනක් වශයෙන් භූ ලක්ෂණාත්මක සිතියමක්, එනයින් නිම්න හා කඳුද, බෑවුම් වල තියුණු බවද පෙන්වන සිතියමකි.


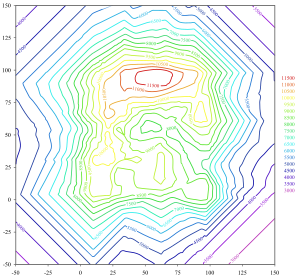
වර්ග
සංස්කරණයභෞතික භූගෝල විද්යාව සහ සාගර විද්යාව
සංස්කරණයචුම්බකත්වය
සංස්කරණයපෘථිවියෙහි චුම්බක ක්ෂේත්රය පිළිබඳ හැදෑරීමේදී, සමක්රාන්තිය හෝ සමක්රාන්ති රේඛාව (ඉහත සමෝච්ච රේඛාවන් වර්ග බලන්න) යන පදයන්ගෙන් අදහස් වන්නේ නියත චුම්බක ක්රාන්තිය, එනම් භූගෝලීය උතුරෙන් චුම්බක උතුර වෙනස් වන ප්රමාණය, සතු රේඛාවක් වෙයි. අකෝණික රේඛාවක් අඳිනු ලබන්නේ ශුන්ය චුම්බක ක්රාන්තිය සතු ලක්ෂ්යයන් හරහාය.
සමානති රේඛාවක් (සමානතිය සඳහා ඉහත සමෝච්ච රේඛාවන් වර්ග බලන්න) විසින් සබැඳනුයේ සමාන චුම්බක අවපාතය සතු ලක්ෂ්යයන් වන අතර, අනානතික රේඛාවක් ඇඳෙනුයේ ශුන්ය චුම්බක අවපාතය සතු ලක්ෂ්යයන් හරහාය.
සමශක්ති රේඛාවක් ('ශක්තිය' යන අරුත ඇති δύναμις හෝ ඩයිනමිස් වෙතින්) විසින් සබැඳනුයේ සමාන චුම්බක බලය සහිත ලක්ෂ්යයන් වෙයි.
මෙයද බලන්න
සංස්කරණයආශ්රිත
සංස්කරණය- ^ කොරන්ට්, රිචඩ්, හර්බර්ට් රොබින්ස්, සහ ජෑන් ස්ටුවර්ට්. වට් ඊස් මැතමැටික්ස්?: ඇන් එලිමෙන්ටර් ඇප්රෝච් ටු අයිඩියාස් ඇන්ඩ් මෙතඩ්ස්. නිව්යෝර්ක්: ඔක්ස්ෆර්ඩ් විශ්වවිද්යාලයීය මුද්රණාලය, 1996. p. 344.
- ^ [1]කොන්ටුවර් ලයින්