පටු දික් සිදුරු කිහිපයකින් හෝ ග්රේටිමකින් සිදු වන විවර්තනය
දික් සිදුරු දෙකක විවර්තන ගැටලුවක රූප සටහනක්. එහි දී තරංග ආයාමයෙන් අර්ධයකට සමාන වන පටි අන්තරයක් විනාශකාරී නිරෝධනයට හේතු වේ. ග්රේටිමක් මඟින් ගවුසීය කදම්භයක විවර්තනය, තනි, ද්විත්ව, ත්රිත්ව, දික් සිදුරු නිරූපණය කරවන අන්වීක්ෂීය ග්රේටිම් සඳහා තියුණු විවර්තන උපරිම ලබා ගැනීමට අභිසාරී කදම්භයක් අවශ්ය වේ.


බහු දික් සිදුරු සැකැස්මක් සිදුරු අවශ්ය තරම් පටු නම්, සරල තරංග ප්රභව රාශියක් ලෙස විස්තර කළ හැක. ආලෝකයේ දී දික් සිදුරු යනු එක් දිශාවකට අපරිමිතව විහිදෙන විවරයකි. එයට ත්රිමාන අවකාශීය ගැටලුවක් ද්විමාන අවකාශීය ගැටලුවක් බවට සරල කර ගත හැක.
සරලම අවස්ථාව වන්නේ එකිනෙකට a දුරකින් පිහිටි පටු දික් සිදුරු දෙකකි. විස්තාරයේ උපරිම හා අවම නිර්ණය කිරීමට අප විසින් ප්රථම දික් සිදුරට හා දෙවන දික් සිදුරට වූ පටි අන්තරය නිර්ණය කළ යුතුය. ෆුවුන්හොෆර් සන්නිකර්ෂණයේ දී, නිරීක්ෂකයා දික් සිදුරුවලට ඉතා ඈතින් සිටින විට සිදුරු දෙකට වූ පථ දුරවල් අතර අන්තරය මෙලෙස දැක්විය හැක.
පථ අන්තරය තරංග ආයාමවල පූර්ණ සංඛ්යාමය ගුණාකාරයක් නම් තීව්රතාවයේ උපරිමයක් ලැබේ.
මෙහි,
- n එක් එක් උපරිමයෙහි අනු පිළිවෙල හඟවන නිඛිලයි.
- λ තරංග ආයාමය
- a දික් සිදුරු අතර දුර
- θ නිර්මාණකාරී නිරෝධනය සිදුවන කෝණය
ඊට අනුරූප අවමයන් ඇත්තේ පථ අන්තරවල පූර්ණ ගුණකාරවලට තරංග ආයාමයෙන් භාගයක් එකතු කළ විටය.
දික් සිදුරු කිහිපයක් සඳහා උපරිම හා අවමවල ස්ථාන වෙනස් නොවේ. දාර, රූපයෙහි දැකිය හැකි පරිදි තියුණුම තිරයෙහි දක්නට ලැබේ. සමාන්තර රේඛා ශ්රේණියක් දිගේ පමණක් පරාවර්තිත වන මතුපිටක් සඳහා ද මෙය සත්ය වේ. එවැනි මතුපිටක් පරාවර්තිත ග්රේටිමක් ලෙස හැඳින්වේ.

රතු ලේසර් ආලෝක දික් සිදුරු 2ක් හා දික් සිදුරු 5ක් තුළින් විවර්තනය සමීකරණය මඟින් විවර්තන කෝණය තරංග ආයාමය මත රඳා පවතින බව පෙනේ. මෙයින් අදහස් කෙරෙන්නේ ආලෝකයේ විවිධ වර්ණ විවිධ දිශාවලට විවර්තනය වන බවයි. එමඟින් ආලෝකය විවිධ වර්ණ සංරචකවලට වෙන් කළ හැකිවේ. වර්ණාවලීක්ෂණයේ දී පරමාණු හා අණුවල හා තරු හා තාරකාන්තර දූවිලි වලාවල ගුණ ඒවා විමෝචනය හා අවශෝෂණය කරන ආලෝක වර්ණාවලි හැදෑරීමෙන් තීරණය කිරීමට ග්රේටිම භාවිතා වේ. විවර්තන ග්රේටිමවල තවත් යෙදීමක් වන්නේ ඒක වර්ණ ආලෝක ප්රභව නිපදවීමයි. මෙය අදාල තරංග ආයාමයට නිර්මාණකාරී නිරෝධන තත්ව ලැබෙන පරිදි දික් සිදුර ආනතව තැබීමෙන් සිදු කළ හැක. ඒක (තනි) දික් සිදුරු විවර්තනය
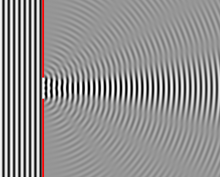

තරංග ආයාමය වඩා වැඩි පළලකින් යුත් දික් සිදුරක් විවර්තනය පෙන්වන්නේ එහි දාරවල දීය. දික් සිදුරු පළල හරහා එක ළඟින් පිළිවෙලට තබා ඇති සරල තරංග ප්රභව රාශියක විවර්තන රටාව සැලකීමෙන් මෙම රටාව පහසුවෙන් තේරුම් ගැනීම හා ගණනය කිරීම සිදු කළ හැක. අපට පහත හේතු දැක්වීම භාවිතයෙන් ලැබෙන තීව්රතා රටාවේ අවමය තීරණය කළ හැක. දී ඇති කෝණයක් සරල ප්රභවයක් දික් සිදුර මධ්යයේ ස්ථාන ගතවී ඇති සරල ප්රභවයක් සමඟ විනාශකාරී නිරෝධනය සිදුවේ නම් වම් කෙළවරේ වූ ප්රභවයට යන්තම් දකුණින් වූ ප්රභවය, මධ්යයේ වූ ප්රභවයට යන්තම් දකුණෙන් වූ ප්රභවය සමඟ විනාශකාරී නිරෝධනය සිදුවේ. මෙම හේතු දැක්වීම මුලු දික් සිදුර පුරාවටම සිදු කරමින්, මුළු දික් සිදුර සඳහා වූ විනාශකාරී නිරොධන තත්වය දික් සිදුරේ පළලෙන් අර්ධයක දුරින් වූ පටු දික් සිදුරු දෙකකින් වන විනාශකාරී නිරෝධනයට සමාන වන බව නිගමනය කළ හැක. මෙහි ප්රතිඵලය වන්නේ ග්රේටිමකින් වන විවර්තනයට වන සමීකරණයට බොහෝ සෙයින් සමාන සමීකරණයකි. වැදගත් වෙනස වන්නේ දැන් එයින් කියවෙන්නේ තීව්රතා ව්යාප්තියේ අවමය වීමයි.
දැන් n යනු 0ට වඩා විශාල නිඛිලයක් වන අතර d යනු සිදුරේ පළලයි.
එම තර්කයම උපරිම සඳහා යෙදිය නොහැක. උපරිමය හා නියම තීව්රතා ව්යාප්තිය තීරණය කිරීමට අශිථිල පිරියමක් අවශ්ය වේ. සියලු බාධා නොවූ පථවල අනුකලනය ආශ්රයෙන් වූ විවර්තන විධි වාදයක් අවශ්ය වේ. එවිට තීව්රතා ව්යාප්තිය දෙනු ලබන්නේ,
මෙහි sinc ශ්රිතය දෙනු ලබන්නේ sinc(x)=sin(x)/x.
බහු ව්යාප්තික පටු දික් සිදුරු
පතන තරංගයේ තරංග ආයාමයට වඩා පළල දික් සිදුරු කිහිපයක එකතුවක් සඳහා අප විසින් වෙනස් සිදුරුවල තරංග නිරෝධනය මෙන්ම එකම සිදුරේ විවිධ ස්ථානවලින් එක තරංග අතර නිරෝධනය ද සැලකිය යුතු වේ. පූර්ණ විනාශකාරී නිරෝධනය සඳහා වූ තනි දික් සිදුරු තත්වයන් හෝ ග්රේටිම තත්වයට ළඟා කරගත හොත් තීව්රතාවේ අවමය ලැබේ. ලැබෙන තීව්රතා ව්යාප්තිය, ග්රේටිම තීව්රතා ශ්රිතයේ හා තනි දක් සිදුරු තීව්රතා රටාවේ ගුණිතයක් බව අශිථිල ගණිතමය පිරියමක් මඟින් පෙන්වා දේ.
එකක පළල d හා එකිනෙක අතර දුර a වූ දික් සිදුරු N සංඛ්යාවක එකතුවක් පහත තීව්රතා රටාව ගෙන දේ.
දික් සිදුරේ පළල ග්රේටිම් පරතරයේ නිඛිලමය සාධකයක් වන අවස්ථාවලදී ග්රේටිම සමඟ පර්යේෂණ සිදු කිරීම වැරදි අනු පිළිවෙල වල්වලට මඟ පෙන්විය හැක. උදාහරණ ලෙස එක් දික් සිදුරක පළල සිදුරු අතර පරතරයෙන් හරි අඩක් නම්, තනි දක් සිදුරු විවර්තන රටාවේ පළමු අවමය සමඟ ග්රේටිම විවර්තන රටාවේ දෙවන උපරිමය සමඟ පෙළ ගැසේ. එවිට මෙම අපේක්ෂිත විවර්තන වැඩිවීම දර්ශනය නොවේ.
http://en.wikipedia.org/wiki/Diffraction#Diffraction_from_an_array_of_narrow_slits_or_a_grating